Dijsktra's Shortest Path Algorithm
Dijsktra's Shortest Path Algorithm
Background

Robot motion planning using Dijsktra's algorithm, Wikipedia
Edsger W. Dijsktra's shortest path algorithm is used to find a list of paths all originating from the same vertex to a map of vertices where all of the paths are of the shortest distance possible. Edsger came up with the idea in 1956.
There are several different variants of this algorithm, in fact, the original only found the shortest distance between two nodes. The much more common variant used today finds what is called a shortest-path tree.
This algorithm has been improved upon by several people, one implemented what is known as a fibonacci heap using a min-priority queue is considered the fastest implementation to date. But there are other faster variants, but they aren't considered to be in the same category. The algorithm is also used in artificial intelligence, specifically in uniform cost search.
Implementation
The way the algorithm works is by using an empty array to store the vertices that have been computed. It starts by computing the distance from the starting vertex to all of the vertices that are connected to it. It selects the smallest one and then inserts that vertex into the array of finished vertices. That finished vertex then becomes a starting point for the next iteration, the distance still starts at the origin, but it calculates the next vertex that is the shortest distance away and then, again, adds it to the list of finished vertices and it too becomes a starting point for the next iteration. The algorithm ends once the list of finished vertices is full.
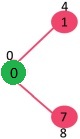
Step 1: calculate the shortest distance from the starting point
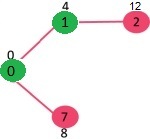
Step 2: Adds the selected vertex to the finished list and then finds the next shortest distance
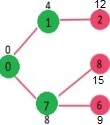
Step 3: Repeat
So lets give it a shot
def findShortestPath_SingleSource(vector_map: list, source_index: int) -> list:
"""Finds the shortest path in a vector-map
vector_map is a 2D array where each column
is a list of that node's distances to other nodes
Finds the shortest path distance from the
source node to every other node on the map, returns
a list of distances where the 0th index is the source
and the ith index is the closest ith node."""
#This is the list I'm going to store the saved vertices in
#The second array is the list of distances to the ith node
sptSet = [0]
sdSet = [0]
#Search Index list
indices = [source_index]
#Fills the arrays with 0's
for i in range(1, len(vector_map)):
sdSet.append(-1)
while len(sptSet) < len(vector_map):
minimum = 2147483647
selected_node = 0
for i in indices:
for j in range(0, len(vector_map[i])):
if vector_map[i][j] != 0:
distance = sdSet[i] + vector_map[i][j]
try:
sptSet.index(j)
except:
if(distance < minimum):
minimum = distance
selected_node = j
indices.append(selected_node)
sptSet.append(selected_node)
sdSet[selected_node] = minimum
return [sptSet, sdSet]
And it worked! I used the sample data given from the site I used as a reference, shown below:
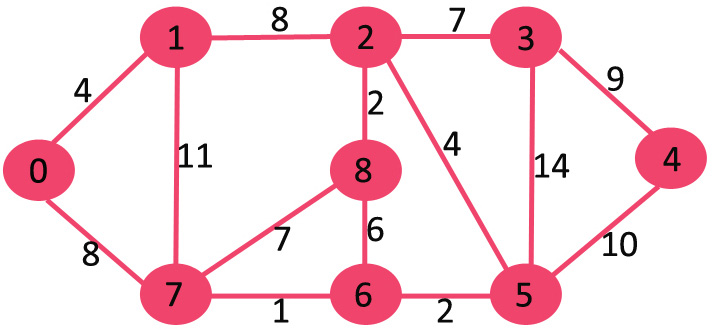
Data layout used for testing, Geeks for Geeks
g = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]]
Output:
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Proof of Concept

Comments
Post a Comment