Heapsort and heaps
Heapsort
There are a lot of algorithms in today's society that are used to do sorting. Heapsort is one of the best and most widely used. According to MIT, the heapsort operates off of 3 things:
Priority Queues
Priority Queues are pretty simple, they're queues, that are ordered, or at leas have methods for extracting either the minimum value, or maximum value from among their members.
Heaps
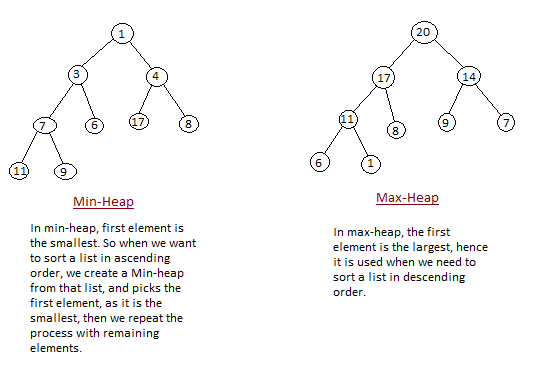
Figure 1, studytonight.com
A heap is an implementation of a priority queue, that is, it is a priority queue that satisfies the heap property. A heap is a representation of a binary tree with the root node being the largest value and all subsequent nodes are larger than their children as well (see figure 1). The nodes in a tree are laid out as follows:
The root index is always 1 (ie. the first element of the array)
Parent(i) = i / 2
Left(i) = 2 * i
Right(i) = 2 * i + 1
(Where i is some index)
Heap Sort
A heap sort uses heaps in order to sort data quickly. The first step is to build a max heap using a recursive function called 'heapify' then, the largest integer is moved to the end of the array, behind the other values that have already been moved there, and then the max heap is built again using a modified array length this time of 1 minus the previous length. I implemented a simple python algorithm below to demonstrate:
Swap function
Simply swaps two values in an array
def swap(given_array: list, index_a: int, index_b: int):
"""Swaps the items in the two locations of the array given specified by index_a and index_b"""
intermediate = given_array[index_a]
given_array[index_a] = given_array[index_b]
given_array[index_b] = intermediate
Max heap function
Builds the max heap out of the given array
def heapify(heap_array: list, heap_size: int, current_index: int):
"""Creates a proper heap out of the given array"""
largest = current_index
left = 2 * current_index + 1
right = 2 * current_index + 2
# If left child is larger than root
if (left < heap_size and heap_array[left] > heap_array[current_index]):
largest = left
# If right child is larger than left
if (right < heap_size and heap_array[right] > heap_array[current_index]):
largest = right
if (largest != current_index):
swap(heap_array, current_index, largest)
heapify(heap_array, heap_size, largest)
Heap sort function
Sorts the given array using the heap sorting method
def heapsort(sort_target: list) -> list:
""" Sorts the given array using the heap sort algorithm"""
# Build the heap (rearrange the array)
for i in range(len(sort_target) // 2 - 1, -1, -1):
heapify(sort_target, len(sort_target), i)
for i in range(len(sort_target) - 1, -1, -1):
swap(sort_target, 0, i)
heapify(sort_target, i, 0)
Example
Lets do an example. Lets say that we're given some array with values of [ 23, 58, 13, 6, 72, 34, 25]. Now, lets take this and sort it using the heap.
Step 1:
First we need to compute the max heap of the given array, we can use the heapify function I supplied above
So starting from i = 7 / 2 - 1 down to 0:
i = 2: heapify(7, 2) -> [23, 58, 34, 6, 72, 13, 25]
i = 1: heapify(7, 1) -> [23, 72, 34, 6, 58, 13, 25]
i = 0: heapify(7, 0) -> [72, 23, 34, 6, 58, 13, 25] (This then recursively calls itself again for heapify(7, 1) which results in below)
[72, 58, 34, 6, 23, 13, 25]
And that concludes step 1!
Step 2:
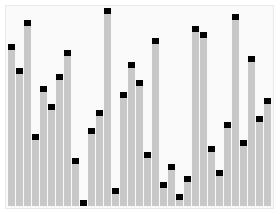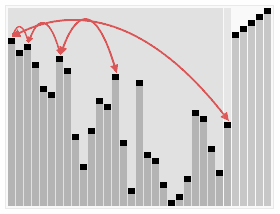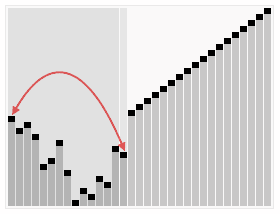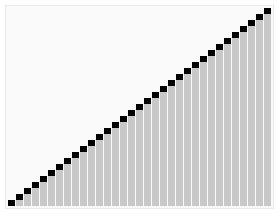
Heapsort process example, Wikipedia
Now we swap the largest value in the array (which will always be in index '0' after we run the heapify function) and swap it for the las position in the array minus 1 position for every iteration (So, first time we put it in the last index, second iteration is index - 1, third iteration index - 2, etc...). This in turn is the equivalent of calling the heapsort function above. To avoid multiple lines of recursion, I will just show the final output of both the swap function, and the heapify function.
So starting from i = 6 down to 0:
i = 6: swap(0, 6) -> [25, 58, 34, 6, 23, 13, 72] and then heapify(6, 0) -> [58, 25, 34, 6, 23, 13, 72]
i = 5: swap(0, 5) -> [13, 25, 34, 6, 23, 58, 72] and then heapify(5, 0) -> [34, 25, 13, 6, 23, 58, 72]
i = 4: swap(0, 4) -> [23, 25, 13, 6, 34, 58, 72] and then heapify(4, 0) -> [25, 23, 13, 6, 34, 58, 72]
i = 3: swap(0, 3) -> [6, 23, 13, 25, 34, 58, 72] and then heapify(3, 0) -> [23, 6, 13, 25, 34, 58, 72]
i = 2: swap(0, 2) -> [13, 6, 23, 25, 34, 58, 72] and then heapify(2, 0) -> [13, 6, 23, 25, 34, 58, 72]
i = 1: swap(0, 1) -> [6, 13, 23, 25, 34, 58, 72] Result: [6, 13, 23, 25, 34, 58, 72]
And that's it!
Proof of Concept

Comments
Post a Comment